在計算機編程中,求解三個數(shù)的平方根之和是一個基礎(chǔ)且實用的任務(wù),廣泛應(yīng)用于數(shù)學(xué)計算、科學(xué)模擬和工程分析等領(lǐng)域。本文將介紹如何使用常見的編程語言(如Python、Java和C++)來實現(xiàn)這一計算,并討論相關(guān)的注意事項。
1. 問題描述
給定三個實數(shù) \(a, b, c\),計算它們的平方根之和,即 \(\sqrt{a} + \sqrt{b} + \sqrt{c}\)。假設(shè)輸入的數(shù)均為非負數(shù),因為負數(shù)的平方根涉及復(fù)數(shù),需要特殊處理。
2. 編程實現(xiàn)示例
以下是幾種主流編程語言的實現(xiàn)方法。
2.1 Python實現(xiàn)
Python以其簡潔的語法和強大的數(shù)學(xué)庫著稱,非常適合此類計算。`python
import math
def sumofsquare_roots(a, b, c):
# 檢查輸入是否為非負數(shù)
if a < 0 or b < 0 or c < 0:
return "輸入必須為非負數(shù)"
# 計算平方根之和
result = math.sqrt(a) + math.sqrt(b) + math.sqrt(c)
return result
示例輸入
a, b, c = 4, 9, 16
print(f"三個數(shù)的平方根之和為: {sumofsquare_roots(a, b, c)}")
# 輸出: 三個數(shù)的平方根之和為: 9.0
`
2.2 Java實現(xiàn)
Java是一種面向?qū)ο蟮木幊陶Z言,適用于跨平臺應(yīng)用。`java
import java.lang.Math;
public class SquareRootSum {
public static double sumOfSquareRoots(double a, double b, double c) {
// 檢查輸入是否為非負數(shù)
if (a < 0 || b < 0 || c < 0) {
throw new IllegalArgumentException("輸入必須為非負數(shù)");
}
// 計算平方根之和
return Math.sqrt(a) + Math.sqrt(b) + Math.sqrt(c);
}
public static void main(String[] args) {
double a = 4, b = 9, c = 16;
System.out.println("三個數(shù)的平方根之和為: " + sumOfSquareRoots(a, b, c));
// 輸出: 三個數(shù)的平方根之和為: 9.0
}
}`
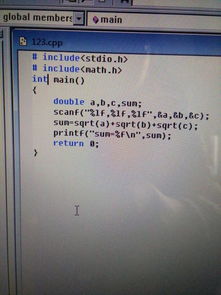
2.3 C++實現(xiàn)
C++以其高性能而聞名,常用于系統(tǒng)級編程。`cpp
#include
#include
using namespace std;
double sumOfSquareRoots(double a, double b, double c) {
// 檢查輸入是否為非負數(shù)
if (a < 0 || b < 0 || c < 0) {
cerr << "輸入必須為非負數(shù)" << endl;
return -1; // 返回錯誤值
}
// 計算平方根之和
return sqrt(a) + sqrt(b) + sqrt(c);
}
int main() {
double a = 4, b = 9, c = 16;
cout << "三個數(shù)的平方根之和為: " << sumOfSquareRoots(a, b, c) << endl;
// 輸出: 三個數(shù)的平方根之和為: 9
return 0;
}`
3. 注意事項
- 輸入驗證:在實際應(yīng)用中,應(yīng)確保輸入的數(shù)非負,否則平方根計算可能產(chǎn)生復(fù)數(shù)或錯誤。可以通過條件判斷來處理負數(shù)輸入,如返回錯誤信息或使用復(fù)數(shù)庫(如Python的
cmath)。 - 精度問題:浮點數(shù)計算可能存在精度誤差,特別是在處理非常大或非常小的數(shù)時。在需要高精度計算的場景中,可以考慮使用高精度數(shù)學(xué)庫(如Python的
decimal模塊)。 - 性能優(yōu)化:對于大量數(shù)據(jù)的計算,可以考慮向量化操作(如使用NumPy庫)或并行計算以提高效率。
4. 擴展應(yīng)用
此計算可以擴展到更多個數(shù),或結(jié)合其他數(shù)學(xué)運算(如求平均值、方差等)。平方根之和在幾何學(xué)、物理學(xué)中也有應(yīng)用,例如計算向量模長或能量值。
5.
通過計算機編程求解三個數(shù)的平方根之和是一個簡單但重要的任務(wù)。不同編程語言提供了相應(yīng)的數(shù)學(xué)函數(shù)(如sqrt)來簡化計算。開發(fā)者應(yīng)根據(jù)具體需求選擇合適的語言和庫,并注意輸入驗證和精度處理,以確保計算的準確性和魯棒性。